Propriétés de la distribution normale
La distribution normale est une distribution de probabilité continue qui est symétrique de part et d’autre de la moyenne, de sorte que le côté droit du centre est une image miroir du côté gauche.
L’aire sous la courbe de la distribution normale représente la probabilité et l’aire totale sous la courbe est égale à un.
La plupart des valeurs de données continues dans une distribution normale ont tendance à se regrouper autour de la moyenne, et plus une valeur est éloignée de la moyenne, moins elle a de chances de se produire. Les queues sont asymptotiques, ce qui signifie qu’elles s’approchent de l’horizon (c.-à-d. l’axe des x) sans jamais le rejoindre complètement.
Pour une distribution parfaitement normale, la moyenne, la médiane et le mode seront la même valeur, représentée visuellement par le sommet de la courbe.
La distribution normale est souvent appelée courbe en cloche parce que le graphique de sa densité de probabilité ressemble à une cloche. Elle est également connue sous le nom de distribution gaussienne, d’après le mathématicien allemand Carl Gauss qui l’a décrite pour la première fois.
Distribution normale vs. distribution normale standard?
Une distribution normale est déterminée par deux paramètres : la moyenne et la variance. Une distribution normale avec une moyenne de 0 et un écart-type de 1 est appelée distribution normale standard.
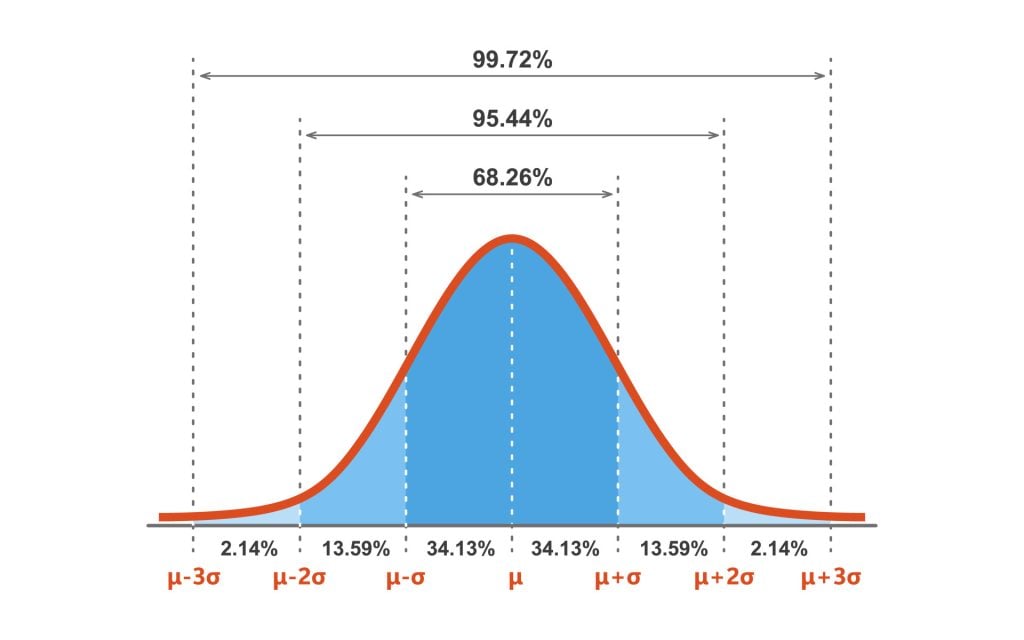
Figure 1.Une distribution normale standard (DNS).
C’est cette distribution qui est utilisée pour construire les tableaux de la distribution normale.
Pourquoi la distribution normale est-elle importante ?
La courbe en forme de cloche est une caractéristique commune de la nature et de la psychologie
La distribution normale est la distribution de probabilité la plus importante en statistique car de nombreuses données continues dans la nature et en psychologie présentent cette courbe en forme de cloche lorsqu’elles sont compilées et représentées graphiquement.
Par exemple, si l’on prélève au hasard un échantillon de 100 personnes, on s’attend à voir apparaître une courbe de fréquence de distribution normale pour de nombreuses variables continues, telles que le quotient intellectuel, la taille, le poids et la pression artérielle.
Les tests de signification paramétriques exigent une distribution normale des points de données de l’échantillon
Les tests statistiques (paramétriques) les plus puissants utilisés par les psychologues exigent que les données soient normalement distribuées. Si les données ne ressemblent pas à une courbe en cloche, les chercheurs peuvent utiliser un test statistique moins puissant appelé statistique non paramétrique.
Conversion des scores bruts d’une distribution normale en scores z
Nous pouvons normaliser les valeurs d’une distribution normale (scores bruts) en les convertissant en scores z.
Cette procédure permet aux chercheurs de déterminer la proportion des valeurs qui se situent à l’intérieur d’un nombre spécifié d’écarts types par rapport à la moyenne (c’est-à-dire de calculer la règle empirique), calculer la règle empirique).
Qu’est-ce que la formule de la règle empirique ?
La règle empirique en statistique permet aux chercheurs de déterminer la proportion de valeurs qui se situent à certaines distances de la moyenne. La règle empirique est souvent appelée règle des trois sigmas ou règle des 68-95-99.7.
Si les valeurs des données d’une distribution normale sont converties en score standard (score z) dans une distribution normale standard, la règle empirique décrit le pourcentage des données qui se situent dans un nombre spécifique d’écarts types (σ) par rapport à la moyenne (μ) pour les courbes en forme de cloche.
La règle empirique permet aux chercheurs de calculer la probabilité d’obtenir au hasard un score à partir d’une distribution normale.
68 % des données se situent dans le premier écart type par rapport à la moyenne. Cela signifie qu’il existe une probabilité de 68 % de sélectionner au hasard un score compris entre -1 et +1 écart-type par rapport à la moyenne.
95 % des valeurs se situent à moins de deux écarts-types de la moyenne. Cela signifie qu’il existe une probabilité de 95 % de sélectionner au hasard une note comprise entre -2 et +2 écarts types par rapport à la moyenne.
99,7 % des données se situeront à l’intérieur de trois écarts types par rapport à la moyenne. Cela signifie qu’il existe une probabilité de 99,7 % de sélectionner au hasard un score compris entre -3 et +3 écarts types par rapport à la moyenne.
Comment vérifier les données
Un logiciel statistique (tel que SPSS) peut être utilisé pour vérifier si votre ensemble de données est normalement distribué en calculant les trois mesures de tendance centrale. Si la moyenne, la médiane et le mode sont des valeurs très similaires, il y a de fortes chances que les données suivent une distribution en forme de cloche (commande SPSS ici).
Il est également conseillé d’utiliser un graphique de fréquence, afin de pouvoir vérifier la forme visuelle de vos données (Si votre graphique est un histogramme, vous pouvez ajouter une courbe de distribution à l’aide de SPSS : Dans les menus, choisissez : Elements > ; Show Distribution Curve).
Les distributions normales deviennent plus apparentes (c’est-à-dire, vous pouvez également calculer des coefficients qui nous renseignent sur la taille des queues de distribution par rapport à la bosse au milieu de la courbe en cloche. Par exemple, les tests de Kolmogorov Smirnov et de Shapiro-Wilk peuvent être calculés à l’aide de SPSS.
Ces tests comparent vos données à une distribution normale et fournissent une valeur p qui, si elle est significative (p < ; .05), indique que vos données sont différentes d’une distribution normale (donc, dans ce cas, nous ne voulons pas d’un résultat significatif et avons besoin d’une pvaleur supérieure à 0,05).
Informations complémentaires
- Définition approfondie de la distribution normale (Académie Kahn)
- Distribution normale standard et règle empirique (Académie Kahn)
- Statistiques pour la psychologie Télécharger le livre
Une distribution normale a-t-elle un kurtosis de 0 ou 3 ?
Une distribution normale a un kurtosis de 3. Cependant, les gens utilisent parfois « l’excès de kurtosis », qui soustrait 3 du kurtosis de la distribution pour la comparer à une distribution normale.
Dans ce cas, l’excès d’aplatissement d’une distribution normale serait de 3 – 3 = 0.
Donc, la distribution normale a un aplatissement de 3, mais son excès d’aplatissement est de 0.
